와... cs231n 쓰다 만거 까먹었당...데헷,,,
정신이 없다...
얼른 시작해보자아!!!
*본문에 있는 ppt 자료는 글쓴이가 제작한 ppt 입니다.
궁금한 점이나 잘못된 부분은 언제든지 댓글로 남겨주세요 :)
먼저 Optimization을 하는 이유는 Stochastic Gradient Decent (SGD)의 문제점을 해결하기 위함이다.
SGD란?

SGD
자 먼저 일반적인 gradient decent 같은 경우에는 full-batch의 training data를 사용하기 때문에 시간이 오래 걸리고 복잡하다. 하지만 SGD에서는 training data를 그림과 같이 mini-batch로 잘라서 gradient decent를 구하기 때문에 시간이 더 빠르지만 전체 데이터에 대한 값이 아니기 때문에 정확도가 떨어질 수 있다는 단점을 가지고 있다.

Problems with SGD 1.
그럼 SGD의 문제점은 어떤게 있을까?
첫번째는 각각의 weight를 업데이트할 때 loss가 주는 영향도가 너무 다르기때문에 비효율적이라는 문제점을 가지고 있다. 위의 그림같은 경우에도 loss가 수평방향의 weight보다 수직방향의 weight에 더 민감하게 반응하는 것을 확인할 수 있다.

Problems with SGD 2.
두번째 문제는 실제 최솟값(global minima)이 아닌 local minima에 빠질 수 있다는 문제점이다. local minima에 빠지게 되면 gradient가 0이 되고 (기울기가 0이기 때문에) backpropagation을 할 때 wight가 전혀 업데이트 되지 않는다는 문제점이 있다.

Problems with SGD 3.
세번째 문제는 mini-batch로 loss 값을 구하기 때문에 gradient의 정확도가 살짝 떨어진다는 점이다. 그렇기 때문에 noise에 취약해서 minimum에 도달하는데 시간이 오래 걸릴 수 있다는 문제점을 가지고 있다.
이러한 문제점을 해결하기 위해서 Optimizer를 사용한다. 아래는 Optimizer의 발달 계보(?)이다.. 보면 이해가 조금 쉬워질 듯!!
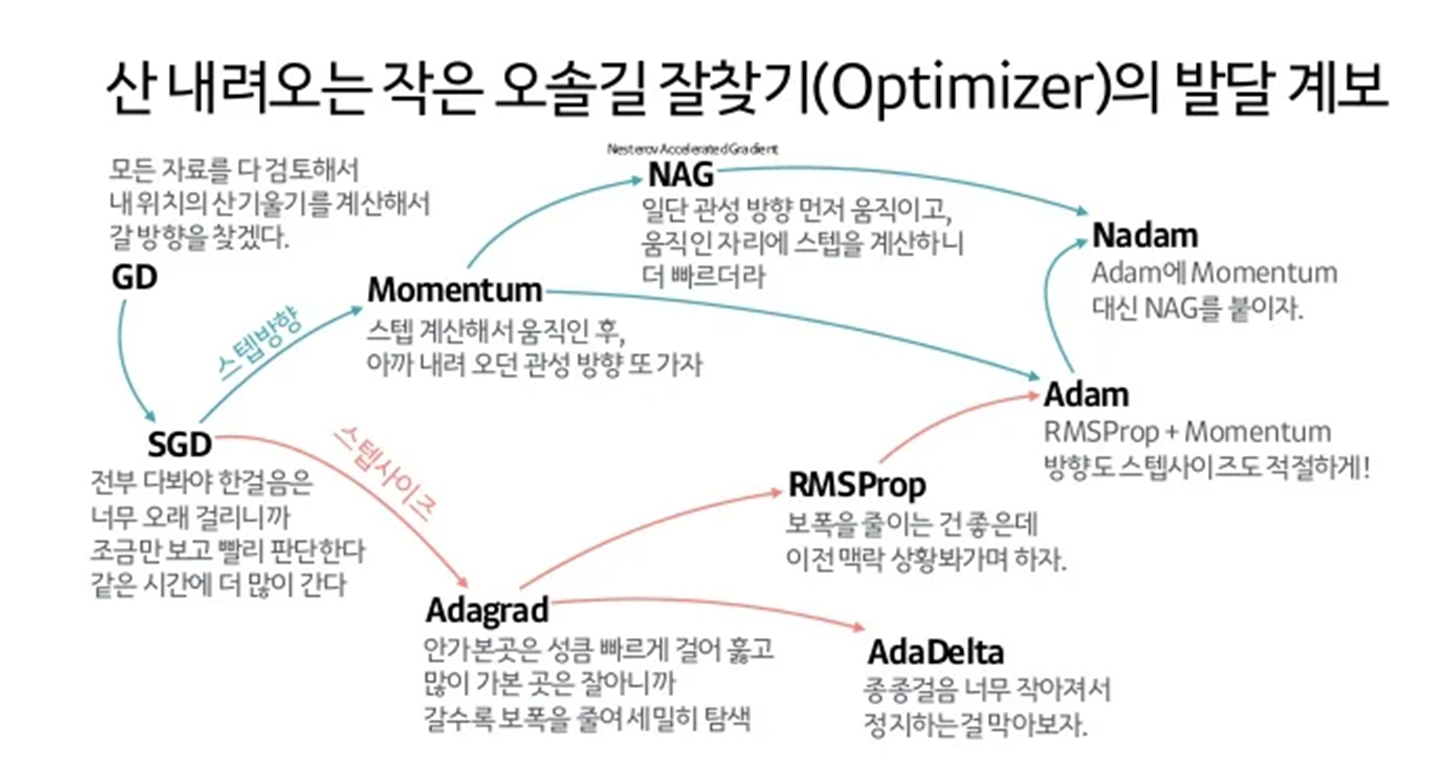
자 그럼 먼저 Momentum부터 시작해서 파란선을 따라가보장..
1. Momentum

Momentum
Momentum은 물리법칙에서 아이디어를 가져온 방법인데 local minima에 빠졌을 때 그 기울기 방향으로 힘을 받아 가속화되도록 한다.
그냥 쉽게 말하면 빨간 점이 공이고 local minima에 빠졌다고 생각해보자. local minima에서 빼내야되는데 local minima로 굴러오게끔 한 기울기만큼 튕겨나가게 하는 것이다. 그럼 빠져나올 수 있겠죠?!?! (아래 그림을 보면 조금 쉽게 이해될 듯 합니당,,, 말로 설명을 잘 못하네요,,,)
이런 Momentum 은 노이즈도 평균화가 된다고 한다.
그런데 이러한 Momentum에 문제점이 있다.

Momentum 문제점
위 그림처럼 local minima에서는 빠져나오는데 (good) 그 관성이 너무 커서 global minima를 지나쳐버릴 수도 있다는 점이다..!!
그래서 이러한 문제점을 해결하기 위해 나온 optimization은 Nesterov Momentum 이다.

Nesterov Momentum 1.
Nesterov Momentum은 먼저 속도의 방향으로 이동한 후에 gradient의 방향으로 이동한다. 속도의 방향이 잘못되었을 경우 gradient의 뱡향을 활용할 수 있도록 해준다. 즉, 속도를 진행한 후에 gradient를 고려하면 global minimum을 뛰어넘는 현상을 줄일 수 있다.

Nesterov Momentum 2.
그림으로 설명하면 다음과 같다. 첫번째 빨간색 점에서는 gradient가 너무 가파라서 local minimum에 도착을해도 뛰어넘을 수가 있다. 그렇기 때문에 local minimum에 도착하기 전에 속도를 조금 늦춰서 local minimum 직전에 멈춰준다. 그 다음에 local minimum으로 가게끔 gradient를 업데이트를 하기 때문에 빠르게 도착할 수 있도록 해준다.
이제는 위 발전단계에서 빨간색 그래프로 가보장

AdaGrad 1.
AdaGrad가 등장한 이유는 각 weight마다 learning rate가 다 같다보니 수렴이 잘 되지 않는다는 문제점때문이다. (그래프처럼 퉁퉁 튀겨나간다) 그렇기 때문에 weight마다 adaptive하게 step size를 적용해주자는 기법이다. 수식은 본래의 gradient descent의 수식이고 빨간색 박스 친 부분이 learning rate이다.

AdaGrad 2.
그래서 AdaGrad에서는 다음과 같은 수식을 사용한다. 위에서 말한 것 처럼 각 weight에 대해서 다른 step size를 가지는 수식이다. 즉 gradient 앞에 곱해지는 값이 달라져야한다는 수식이다. 즉 minimum에 가까워질수록 learning rate를 줄여서 local minimum을 지나치지 않고 찾을 수 있도록 하는 방법이다.
수식은 제대로 이해한지는 모르겠지만 일단 G_t 수식을 보게되면 이전 gradient에 J(theta t))를 제곱해주었기 때문에 현재 gradient의 값이 클수록 learning rate (theta_t+1)의 값은 작아지고 반대로 gradient의 값이 작을 수록 theta_t+1은 커질 것이다.
즉, local minimum에 가까워질수록 learning rate가 작아질 것이다.
여기서도 문제가 있는데!! learning rate가 너무 빠르게 줄어들다보니까 오른쪽 그래프에서 볼 수 있듯이 아직 local minima에 도착하지 않았는데 멈춰버리는 문제가 생기게 된다.
그래서 등장한게 RMSProp!!

RMSProp
위의 AdaGrad와 식이 비슷하지만! gradient 식을 보게 되면 감마라는 decay rate를 곱해주게 된다. learning rate의 속도를 줄여주게 된다.
추가적으로 Adam 이라는 optimization이 있는데 이건 RMSProp의 장점과 Momentum의 장점을 합친 것이다.

Adam
learning rate를 구하는 부분에서 이전 step의 gradient를 사용하는 관성을 사용하되 minimum을 넘어서지 않도록 decay rate를 곱해주는 것이 Adam이다.
끝!!
아무튼 결론은 각자의 모델에 적합한 optimization을 사용하는게 최고라고 하셨음, , ,
많이 부족하지만 내 인생 첫 ML 공부 얼레벌레 끝...!!!
'STUDY' 카테고리의 다른 글
| [리눅스] RAM 캐시 메모리 정리 (0) | 2024.02.21 |
|---|---|
| [SYSBENCH] SYSBENCH Workload 사용해보기 (0) | 2023.11.28 |
| CS231n (Activation Function ~ Regularizaton) (2) | 2023.10.16 |
| [ch.3] Bellman Equation (0) | 2022.02.15 |
| [ch.2] Markov Decision Process (0) | 2022.02.08 |