방학이 시작됐다... 지옥같은 방학... 대학원생은 방학이 싫어요,,,
이번 달은 스터디, 논문 세미나로 갈릴 예정
그 첫번째 여정 - CS231n
일단 이 강의는 vision 수업이기 때문에 나한테 필요한 부분만 골라골라서 공부했다는 점,
그리고 글에 부족한 점이 굉장히 많다는 점 참고 부탁드립니다...
+) 사진에 있는 ppt는 글쓴이가 제작한 ppt 내용입니다.
Activation Functions
Activation fuction을 시작하기 위해 퍼셉트론 개념을 먼저 정리해보자.
단층 퍼셉트론은 입력층에 wight 하나만을 곱해서 출력으로 내는 레이어다.

단층 퍼셉트론
다층 퍼셉트론은 입력층과 출력층 사이에 1개 이상의 hidden layer가 있는 레이어이다.

다층 퍼셉트론
이러한 다층 퍼셉트론에서 어떤 데이터들을 classification할 때 우리는 대체로 데이터들끼리 and, or, xor 연산을 한다.
이 때 아래 그림과 같이 and, or 연산을 한 경우에는 하나의 선으로도 데이터들을 classification이 가능하지만 xor 연산을 한 경우에는 하나의 선으로는 classification이 불가능 하다. 빨간색 선과 같이 두 개의 선으로 classification이 가능하다.

xor 연산 시 classificaion 하는 방법
하지만 이렇게 두 개의 선으로 classification을 하게 되는 경우, 함수가 두 개 이기 때문에 backpropagation을 할 경우 계산이 복잡해진다. (backpropagation 관련한 개념은 생략하도록 하겠다.)
그렇기 때문에 다음 그림과 같이 비선형적인 함수를 통해 classification을 하도록 하고 선형적인 함수(xw+b) 를 비선형 함수로 만들기 위해 사용하는 function이 activation function이다.

xor 연산 시 비선형 함수로 classification 함.
자 드디어 Activation Function의 첫번째.
Sigmoid function이다.

Sigmoid Function
Sigmoid는 0과 1사이의 값으로 나타내는 함수이며 세가지의 문제점이 있다.

Sigmoid의 첫번째 문제점
첫번째 문제점은 gradient가 0이 되어서 뉴런이 saturated 된다는 점이다.
이게 무슨 말이냐?!
ppt의 왼쪽 그래프에서 볼 수 있듯이 sigmoid는 너무 작은 데이터의 값을 넣거나 너무 큰 값의 데이터를 넣으면 함수의 기울이(gradient)가 0이 된다. 그렇게 되면 backpropagation을 하는 과정에서 당연히 loss값을 전달해주지 못하고 weight가 업데이트 되지 못할 것이다. 이것을 수업에서는 gradient가 kill 되고 뉴런이 saturated된다고 표현한다.

Sigmoid의 두번째 문제점
두번째 문제점은 'not zero-centered' 이다. 아마 이 강의에서 말하는 not zero-centered란 모든 y값이 양수라는 의미인 것 같다. 모든 y의 값이 양수일 경우에 무슨 문제가 생길까!
그래프 밑에 써논 수식은 f(x)라는 objective function에서 backpropagation을 하는 과정이다. f(x) 함수에 대해서 wi에 대한 편미분을 하게 되면 xi가 나오게 된다. 그런데 여기서 xi는 이전 step에서의 sigmoid function의 결과값이기 때문에 무조건 양수일 수 밖에 없다. 그렇게 되면 chain rule을 거친 두번째 식에서 Loss에 대한 f(x) 와 wi의 편미분 값은 늘 양수이거나 음수이게 된다. (양수 * 양수 = 양수, 음수 * 양수 = 음수)
그렇게 되면 움직일 수 있는 gradient의 방향은 1사분면과 3사분면 두 방향 뿐이다. 오른쪽 그림에서 파란색 화살표가 gradient가 나아가야할 방향인데 1사분면과 3사분면 방항으로밖에 움직이 못하므로 실제 gradient는 빨간색 화살표처럼 지그재그 모양으로 움직이게 될 것이다. 그러면? 너무너무 비효율적이게 된다..
세번째 문제는 지수함수의 계산이 컴퓨터에서 계산하는 과정이 넘 복잡하기 때문에 expensive하다는 문제점이다.
두번째는 tanh(x) 함수이다.

tanh function
tanh 함수는 결과값은 -1,1 사이의 값으로 나타내며 앞에서 말했던 not zero centered의 문제점은 생기지 않는다.
하지만 그래프에서 확인할 수 있듯이 앞 서 설명했던 gradient가 0이 되어서 backpropagation 과정에서 뉴런이 업데이트되지 않는 (saturated) 문제는 여전히 존재한다.
세번째는 ReLU 함수이다.

ReLU Function
ReLU는 max(0,x)의 연산을 거치는 함수이며 그렇기 때문에 계산이 굉장히 편리하다. 그리고 수렴하는 속도가 sigmoid나 tanh 함수보다 6배 정도 빠르다. 추가적으로 양수 부분에서는 saturated 되지 않는다는 장점을 가지고 있다.
하지만 음수 부분에서는 여전히 saturated된다는 단점과 not zero-centered 의 문제점을 가지고 있다.
이런 ReLU 함수는 데이터 전처리 과정에서 음수의 데이터를 걸러내기 위해 사용될 수 있지 않을까?
네번째는 Leaky ReLU 함수이다.

Leaky ReLU
Leaky ReLU는 ReLU 함수에서 x값에 0.01 파라미터를 곱해주는 함수이다. Leaky ReLU도 계산식이 간단하기 때문에 효율적이며 sigmoid, tanh 함수보다 수렴 속도가 빠르다는 장점을 가지고 있다. 추가적으로 그래프에서 확인할 수 있듯이 양수에서도 음수에서도 saturated되지 않는다는 장점을 가지고 있다! 추가적으로 PReLU도 이야기 하는데 x값 앞에 붙는 파라미터도 학습을 시키는 함수는 PReLU라고 한다고 이야기 한다.
세미나에서 추가적으로 들었던 이야기는 각각의 activation function마다 적절한 데이터 전처리가 있으며 현재 사용하지 않는 함수가 있거나 그렇지는 않다고 한다. (수업에서는 현재 sigmoid는 사용하지 않는다 이런식으로 얘기했던 것으로 기억한다.)
Weight Initialization
다음 내용은 weight 초기화인데 .. 사실 세미나에서는 이 내용은 굳이 발표하지 않아도 된다고 하셨기 때문에 코멘트를 듣지 못해서 아래 내용은 확실하지는 않으며 간단하게만 설명하려고 한다.

Weight Initialization
자! 먼저 w를 0으로 초기화한다고 생각해보자. 그럼 어떻게 될까!!
w가 0이 되면 backpropagation과정에서 loss를 전달해주지 못하고 계속 같은 값 (bias)만 업데이트 될 것이다.
그렇기 때문에 수업에서는 먼저 w에 랜덤한 작은 숫자를 넣어서 테스트 해보자고 한다. 왼쪽코드와 같이 activation function은 tanh를 사용하였고 w는 랜덤한 숫자에 0.01의 편차를 곱해주게 된다. 결과는?
오른쪽 첫번째 그래프는 평균 그래프, 오른쪽은 표준편차 그래프, 아해 그래프는 결과값의 분포도 이다.
tanh은 zero-centered 함수였기 때문에 평균은 0에 고르게 분포하는 것을 확인할 수 있다. 하지만 표준편차는 layer가 더해질 때마다 점점 0으로 수렴하고 있으므로 데이터 분포도 일정한 구간에만 모여있는 것을 확인할 수 있다.

Weight Initialization
그럼 반대로 아주 큰 값을 넣으면 어떻게 될까.. 0.01대신 편차를 1.0로 넣어주었을 때는 그래프 설명에서 볼 수 있듯이 gradient가 0이 되고 saturated되어서 데이터의 분산이 -1과 1에 모여있는 것을 확인할 수 있다.
그래서 그럼 뭐 어떡하라고..

Xavier initialization
그래서 나온게 xavier initialization이다. 랜덤으로 뽑은 w의 값을 데이터 input의 수로 나누어서 node의 갯수를 normalize하는 방법이다. 그렇기 때문에 input 데이터의 수가 적으면 w값은 커지고 반대로 input 데이터의 수가 많으면 w값은 작아지도록 한다. 하지만 이 방법이 ReLU에게는 적용이 되지 않는다고 한다.
ReLU는 음수의 데이터들은 모두 gradient가 0으로 수렴되기 때문에 He 라는 초기화 방법에서는 input 데이터를 2로 나눈 뒤에 w의 값을 나누어 준다. (데이터들이 반갈되니까?... 아마도.... 아직도 잘 모르겠다ㅠ)

He
음.. 아무튼 weight 초기화 부분은 더 공부해봐야할 것 같다.
Hyperparameter Optimization
hyperparameter optimization이다... 강의에서는 최적화 방법으로 Cross-validation strategy를 사용한다.
이게 뭐냐면,,,
일단 처음에는 적은 에포크를 가지고 실험하면서 어떤 파라미터를 최적화할지 결정한 후에 running time을 늘리면서 파라미터를 최적화해가는 방법을 말한다.
그래서 강의에서는 다음과 같은 테스트를 진행한다.

Hyperparameter Optimization
맨 처음에는 regularization 값과 learning rate를 각각 (-5, 5) (-3, -6)으로 지정하고 코드를 돌렸을 때 제일 좋은 결과를 나타내는 값의 주변으로 값을 변경해가면서 하이퍼파라미터를 최적화해 나간다. 그렇게 했을 때 실제로 53% 정도 좋은 결과를 나타낸다고 한다..

그럼 이렇게 맨 처음에 파라미터 값을 넣을 때는 어떤 방식으로 넣을까?
두가지 방법이 있다.
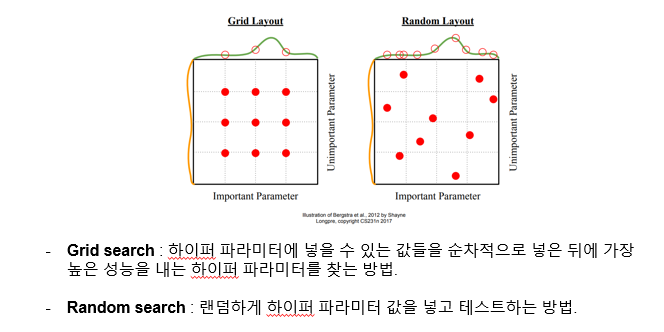
첫번째는 Grid search 방법이다. 피피티에 적혀있듯이 , 하이퍼 파라미터에 넣을 수 있는 값들을 어떤 범위를 정해놓고 순차적으로 넣어보고 가장 높은 성능을 내는 하이퍼 파라미터를 찾아낸다. 이런 경우에는 적합한 파라미터가 다른 위치에 (빨간점을 보았을 때) 있을 수도 있는데 찾아내기 힘들기 때문에 정확도가 떨어진다는 단점이 있다. 즉 놓치는 간격이 너무 많다는 단점이 있다.
+) Cross Validation
세미나에서 추가적으로 공부하라고해서 찾아본 내용
모델을 훈련시킬 때 원래 train set으로 훈련시키고 test set으로 모델이 잘 훈련되었는지 확인한다. 그런데 계속 이렇게 test set에 대해서만 성능을 검증하면 이 test set에 대해서만 좋은 성능을 내게 될 수도 있다.
즉, test set 에 overfitting 된다.
이를 막기 위해서 train 과 test 사이에 validation 과정을 집어넣어서 train이 얼마나 잘됐는지 확인하는 과정!
Regularization
regularization은 딥러닝 모델의 overfitting을 막는 방법이다. overfitting이란 위에서도 작성했는데! 하나의 data set에만 너무 지나치게 학습되어서 실제 데이터에 대한 오차가 증가하는 경우 발생하는 문제점이다.

Overfitting
1. Weight Regularication

L1, L2 Regularization
그 유명한 엘원 엘투 ,, 근데 난 매우 간단하게 설명할 것이기 때문에 자세한 내용 (Lasso, Ridge에 대한...)은 추가적으로 찾아보는 것을 추천...
일단 우리의 목적은 loss 값을 최소화하는 것이다. 근데 그 과정에서 특정 w의 값이 커질 수 있고 이게 overfitting을 일으킬 수 있다. 이걸 해결해주기 위해서 L1 에서는 w값의 절댓값들을 모두 더해줌으로써 규제를 주고 이 값도 최소가 되도록 한다. 이 더해준 식이 Lasso...
L2에서는 w값을 제곱한 값들을 모두 더해줌으로써 규제를 주는데 이게 Ridge이다. 추가적으로 모델을 학습시킬 때 w값에 예민하게 반응하길 원한다면 w값을 제곱해주는 L2를 사용하는 것이 효율적이다.
2. Dropout

Dropout
Dropout은 랜덤하게 일부 node를 0으로 지정하는 것이다. 이렇게되면 backpropagation 과정에서 weight의 update가 끊기게 된다. Dropout을 했을 때의 장점은 이건 스탠포드 강의가 아니라 다른 강의에서 실제로 사용한 표현인데 .. node가 많으면 '아 나 하나쯤이야 loss값 조금 틀리게 전달해도 되겠지~ 옆에 애가 제대로 하면 되자너~' 라고 하는데 그 옆 node가 사라지면 (일하는 node 수가 줄어들면) 정신 똑띠 차리고 일을 열심히 할 것이다... 그래서 정확도가 높아지고 효율성이 좋아진다..고 표현하였다. . . . . . 근데 무슨 의미인지 확실히 알겠음 ㅎㅋㅎㅋ
아!! 너무 힘들어서 나머지는 새로 써야겠다...!!!!!!!
다음은 Fancier Optimization으로 momentum, Adagrad, Adam 등등의 내용을 작성해보겠다!!
끝!! 어렵다 어려워!!
'STUDY' 카테고리의 다른 글
| [SYSBENCH] SYSBENCH Workload 사용해보기 (0) | 2023.11.28 |
|---|---|
| CS231n (Fancier Optimization) (0) | 2023.10.16 |
| [ch.3] Bellman Equation (0) | 2022.02.15 |
| [ch.2] Markov Decision Process (0) | 2022.02.08 |
| [ch.1] Reinforcement Learning (0) | 2022.02.08 |